| מחבר |
 נושא חפש נושא חפש  אפשרויות הודעה אפשרויות הודעה
|
crazycrickett 
חבר חדש

הצטרף: 10/יוני/2006
מצב מקוון: מנותק
מאמרים: 31
|
 ציטוט ציטוט  תגובה תגובה
 נושא: בעיה באלגברה נושא: בעיה באלגברה
פורסם: 06/אוגוסט/2009 ב- 20:25 |
היי,
x^2+2(a+1)x+(a^2+2a+1)=0 ?=x+1 1)a- 2)a חלקי 2 3)2a 4)a^2 הייתי שמח לדעת איך לפתור את זה בצורה אלגברית. 
|
 |
tsofi 
חבר חדש


הצטרף: 16/יוני/2009
מצב מקוון: מנותק
מאמרים: 34
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 06/אוגוסט/2009 ב- 21:29 פורסם: 06/אוגוסט/2009 ב- 21:29 |
הדרך שלי- פשוט לפתור את המשוואה. שים לב שזו משוואה ריבועית, גם אם האיברים טיפה מסובכים.
אז לפי נוסחת הכפל המקוצר יוצא פתרון יחיד והוא: x=-a-1.
מוסיפים 1 לכל צד במשוואה ויוצאת תשובה מספר 1).
אני חושבת שאם אין שום דרך ברורה איך לפתור, אפשר להבין שכשנמצא את הערכים של X התשובה תצוץ לפתע...
אבל אני לא מומחית, אולי יש דרך יותר מהירה.
בהצלחה!
|
 |
crazycrickett 
חבר חדש

הצטרף: 10/יוני/2006
מצב מקוון: מנותק
מאמרים: 31
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 06/אוגוסט/2009 ב- 21:50 פורסם: 06/אוגוסט/2009 ב- 21:50 |
|
אני לא מבין איך נוסחת הכפל המקוצר מביאה אותך למצב x=-a-1 , את יכולה לנמק?
|
 |
tsofi 
חבר חדש


הצטרף: 16/יוני/2009
מצב מקוון: מנותק
מאמרים: 34
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 06/אוגוסט/2009 ב- 22:08 פורסם: 06/אוגוסט/2009 ב- 22:08 |
אוי, סליחה...
התכוונתי לנוסחת השורשים.
פשוט תציב.
|
 |
assafy 
חבר בכיר


הצטרף: 01/ינואר/2009
מצב מקוון: מנותק
מאמרים: 968
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 06/אוגוסט/2009 ב- 23:04 פורסם: 06/אוגוסט/2009 ב- 23:04 |
|
אני חושב שחבל לפתור שאלה כזו בדרך אלגברית. זה רק מאריך את הדרך
לעומת זאת, אם מציבים X=0, זה ממש מקצר את הדרך
עד הסוגריים האחרונים הכל שווה אפס, ולמעשה נשארנו עם:
a^2+2a+1=0
מעבירים את 1 לצד השני, וזה יוצר
a^2+2a=-1
לא צריך להיות יותר מדי חד עין כדי לראות שהתשובה היא ש-A שווה למינוס 1
בתשובה, אחרי שכאמור הצבנו ש-X שווה לאפס, אנחנו צריכים לבדוק (בהצבת A=-1, כפי שהמשוואה יצאה לנו) מתי התשובה תהיה 1 (הרי 0+1=1).
ומהר מאוד רואים שהתשובה היא תשובה מספר 1 (מקווה שאני צדוק באמת P: ).
לדעתי לפתור אלגברית זה גיהנום בשאלה הזו, בעיקר בהתחשב בעובדה שצריך להתמודד עם כל כך הרבה משתנים, וזה עוד לפני שמדברים על הזמן שהצבה חוסכת לנו
|
 |
crazycrickett 
חבר חדש

הצטרף: 10/יוני/2006
מצב מקוון: מנותק
מאמרים: 31
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 06/אוגוסט/2009 ב- 23:33 פורסם: 06/אוגוסט/2009 ב- 23:33 |
תודה רבה ,הבנתי את התרגיל.
אך בכל זאת רציתי לדעת מהי נוסחת השורשים?
|
 |
tsofi 
חבר חדש


הצטרף: 16/יוני/2009
מצב מקוון: מנותק
מאמרים: 34
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 06/אוגוסט/2009 ב- 23:59 פורסם: 06/אוגוסט/2009 ב- 23:59 |
אסף- באמת אפשר להציב פשוט 0? זה לא מספר שעלול לקלקל הכל?
נוסחת השורשים זו הנוסחא הזו: 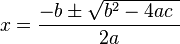 היא נותנת את שתי האפשרויות שX יכול לקבל (לפעמים הוא יקבל רק ערך 1- אם יצא 0 מתחת לשורש, או שום ערך- אם יצא מספר שלילי מתחת לשורש)
משתמשים בה המון בתיכון...
|
 |
crazycrickett 
חבר חדש

הצטרף: 10/יוני/2006
מצב מקוון: מנותק
מאמרים: 31
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 07/אוגוסט/2009 ב- 00:03 פורסם: 07/אוגוסט/2009 ב- 00:03 |
תודה
|
 |
אלעד שווייצר (פסיכו) 
מנהל פסיכו


מנהל הפורום
הצטרף: 02/מאי/2006
כתובת: תל אביב
מצב מקוון: מנותק
מאמרים: 18183
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 07/אוגוסט/2009 ב- 00:06 פורסם: 07/אוגוסט/2009 ב- 00:06 |
את נוסחת השורשים לא צריך לפסיכומטרי.
הרעיון בתרגיל הוא לשים לב שהחלק האחרון זה מנוסחת כפל מקוצר ואפשר לסגור אותו.
a2 +2a + 1 = (a+1)2
ואז התרגיל הוא:
x2 + 2(a+1)x + (a2 + 2a + 1) = 0
x2 + 2(a+1)x + (a+1)2 = 0
ואז שוב יש כפל מקוצר, כשהאיבר הראשון זה x והשני זה a+1
ויוצא ש- x+a+1 = 0
|
|
|
 |
assafy 
חבר בכיר


הצטרף: 01/ינואר/2009
מצב מקוון: מנותק
מאמרים: 968
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 07/אוגוסט/2009 ב- 08:49 פורסם: 07/אוגוסט/2009 ב- 08:49 |
פורסם במקור ע"י tsofi
אסף- באמת אפשר להציב פשוט 0? זה לא מספר שעלול לקלקל הכל? |
רק במקרים הבאים אי אפשר להציב אפס: 1. כשאומרים לנו מראש שתחום ההגדרה של משתנה מסוים הוא שונה מאפס 2. כשיש משתנה במכנה, ואז אסור להציב אפס, כי אי אפשר לחלק באפס בכל שאר המקרים אפשר להציב מה שרוצים, לרבות אפס. מה שכן-שימי לב שלא תמיד כדאי להציב אפס, ולפעמים לא כדאי להציב בכלל. עם זאת, במקרה כמו זה, לפתור אלגברית לא מומלץ לדעתי, ובכל מקרה-אחרי שמתרגלים הרבה שאלות, מצליחים להבין מתי כדאי להציב, מתי כדאי לפתור אלגברית, ואם להציב-מה בדיוק להציב
|
 |
אלעד שווייצר (פסיכו) 
מנהל פסיכו


מנהל הפורום
הצטרף: 02/מאי/2006
כתובת: תל אביב
מצב מקוון: מנותק
מאמרים: 18183
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 07/אוגוסט/2009 ב- 14:00 פורסם: 07/אוגוסט/2009 ב- 14:00 |
אסף, האמת היא שבמקרה הזה אמנם אפשר היה להציב אפס, אבל זו לא הדרך המומלצת.
רק במקרה הצלחת למצוא את התשובה כי "ראית" את הפתרון למשוואה בסוף.
אם היתה יוצאת משוואה אחרת, לא היית יכול לדעת מה התשובה.
בשאלה כגון זו לא מומלץ להציב אפס, או כל מספר אחר.
הסיבה היא שהצבת מספרים צריכה לעמוד בשני תנאים:
1) בתשובות יש נעלמים כך שאם נציב נוכל להציב גם בתשובות.
2) מדובר בביטוי ולא במשוואה.
במקרה זה מדובר במשוואה, ולכן אסור להציב סתם מספרים - אנחנו לא יודעים שההצבה של המספר היא אכן נכונה ותפתור את התרגיל.
כאשר מדובר במשוואה, ניתן להציב כל מספר, שכן אין צורך להגיע לתשובה ספציפית כלשהי
|
|
|
 |
yossifun 
חבר מסור


הצטרף: 22/ינואר/2009
מצב מקוון: מנותק
מאמרים: 82
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 09/אוגוסט/2009 ב- 15:05 פורסם: 09/אוגוסט/2009 ב- 15:05 |
|
בלבלת אותי אלעד
במשוואה אסור להציב מה שרוצים ובביטוי מותר להציב כל מספר?
במשוואה נציב מספרים מהתשובות?
|
 |
אלעד שווייצר (פסיכו) 
מנהל פסיכו


מנהל הפורום
הצטרף: 02/מאי/2006
כתובת: תל אביב
מצב מקוון: מנותק
מאמרים: 18183
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 10/אוגוסט/2009 ב- 00:37 פורסם: 10/אוגוסט/2009 ב- 00:37 |
מצטער שבלבלתי, אנסה לעשות סדר -
במשוואה אסור להציב מספרים!
למה? כי למשוואה יש פתרון מסוים קבוע. אנחנו לא יכולים להחליט להציב מספר כי לא בטוח שזה המספר הנכון.
בביטוי מותר להציב איזה מספר שרוצים - בכל הצבה הערך של הביטוי יהיה שונה.
|
|
|
 |
yossifun 
חבר מסור


הצטרף: 22/ינואר/2009
מצב מקוון: מנותק
מאמרים: 82
|
 ציטוט ציטוט  תגובה תגובה
 פורסם: 10/אוגוסט/2009 ב- 14:42 פורסם: 10/אוגוסט/2009 ב- 14:42 |
|
עשית סדר עכשיו תודה רבה
|
 |

